The goal of knnwtsim is to provide a package to share
and implement a forecasting methodology using k nearest neighbors (KNN)
primarily for situations where the response series of interest can be
predicted by a combination of its’ own recent realizations, its own
periodic patterns, and by the values of one or multiple exogenous
predictors.
The functions of this package are focused primarily into two
components. The first being calculation of a similarity measure which
takes into account all three factors listed above (S_w),
and can weight the degree to which each component contributed to the
overall similarity. The second being the usage of this measure to
identify neighbors and perform KNN regression. For a more formal
discussion of the methodology used and the key user facing functions in
knnwtsim please see Trupiano (2021)
<arXiv:2112.06266v1>.
S_wThe Similarity measure I have formulated for incorporating the three factors listed above is:
S_w = alpha * S_t + beta * S_p + gamma * S_x
Where S_t is the metric used to calculate the similarity
matrix generated by StMatrixCalc to measure similarity in
terms of pure recency between all observations. alpha is
the weight between 0-1 assigned to this matrix in the calculation of
S_w.
S_p is the metric used to calculate the similarity
matrix generated by SpMatrixCalc to measure similarity in
terms of where each observation falls along a periodic cycle relative to
all others. beta is the weight between 0-1 assigned to this
matrix in the calculation of S_w.
S_x is the metric used to calculate the similarity
matrix generated by SxMatrixCalc to measure similarity
between all observations in terms of the values of one or more exogenous
predictors associated with a given observation. gamma is
the weight between 0-1 assigned to this matrix in the calculation of
S_w.
The function SwMatrixCalc calls each of the previous
similarity matrix functions to generate the final matrix to use in
knn.forecast.
The weights alpha, beta, and
gamma are recommended to be set so that they sum to 1. In
this case each element of final similarity matrix should also be between
0-1, with the diagonal elements being equal to 1.
Initially S_t, S_p, and S_x
are calculated as dissimilarities, D_t, D_p,
and D_x. They are then transformed to similarities by the
formula 1 / (D+1), where D is any
dissimilarity measure. This also ensures each element of the similarity
matrices fall in the range (0,1], with 1 representing the
greatest similarity, and the values approaching 0 the least.
When StMatrixCalc generates the intermediate
dissimilarity matrix using D_t, it calls the function
TempAbsDissimilarity for each pairwise combination of the
input vector. Which provided the time orders of two points
y_i and y_j, where the time orders are
i and j.Then
TempAbsDissimilarity(i, j) will return the absolute
difference between the two, i.e abs(i - j).
When SpMatrixCalc generates the intermediate
dissimilarity matrix using D_p, it calls the function
SeasonalAbsDissimilarity for each pairwise combination of
the input vector. This function takes the values corresponding to the
periods of two points in an overall periodic/seasonal cycle, and the
total number of periods in a cycle. Where we have two points
y_i and y_j with p_i and
p_j representing the corresponding period of those points,
and a total of p_max periods in a full periodic cycle. The
value returned by SeasonalAbsDissimilarity(p_i, p_j, p_max)
will be min(DirectDis, AroundDis) where
DirectDis <- abs(p_i - p_j) and
AroundDis <- abs(min(p_i, p_j) - 1) + abs(p_max - max(p_i, p_j)) + 1.
This formulation is based on the idea that generally the periods at
the very end and very beginning of a cycle should be fairly similar. To
clarify through an example, in a monthly cycle where 1 represents
January and 12 represents December, these two months are generally more
similar to each-other than either are to July at period 7. Continuing
with this monthly example, if we have three points which occur in
January, March, and November: p_i = 1,
p_j = 3, p_k = 11 with
p_max = 12. Then
SeasonalAbsDissimilarity(p_i, p_j, p_max) = 2,
SeasonalAbsDissimilarity(p_i, p_k, p_max) = 2, and
SeasonalAbsDissimilarity(p_j, p_k, p_max) = 4.
Finally, SxMatrixCalc uses the stats::dist
function to produce the intermediate dissimilarity matrix using
D_x, for an input matrix or vector using the method
indicated by the XdistMetric argument of
SxMatrixCalc. Naturally, this limits D_x to
the methods available in stats::dist.
K nearest neighbors forecasting is implemented in this package
through the function knn.forecast. Using a provided
similarity matrix, which is not required to be calculated using
S_w specifically, the function will perform K Nearest
Neighbors regression on each point in a specified index
f.index.in, returning the mean of the identified,
k.in, neighbors in the response series
y.in.
Mathematically the estimate for a given point y_t is
formulated as the mean of the previous points in the series
y_i identified to be in the neighborhood of
y_t, K(y_t).
In the neighborhood K(y_t) will be the k
observations of y_i with the highest similarity to
y_t of all eligible members of the time series, meaning
i < t. Currently in knn.forecast this
eligibility constraint is enforced by only considering the rows of the
similarity matrix at indices which are not present in
f.index.in when selecting neighbors while performing KNN
regression on each point in f.index.in, thus preventing the
corresponding points in y.in at those indices from being
selected as neighbors. Furthermore, rows and columns of
Sim.Mat.in at indices greater than the maximum value of
f.index.in will be removed.
You can install the most recent stable version from CRAN with
install.packages("knnwtsim")You can install the development version of knnwtsim from GitHub with:
# install.packages("devtools")
devtools::install_github("mtrupiano1/knnwtsim")kThis is a basic example which shows a full forecasting workflow if
the weights to use in the generation of S_w, and the
hyperparameter k are known:
library(knnwtsim)
# Pull a series to forecast
data("simulation_master_list")
series.index <- 15
ex.series <- simulation_master_list[[series.index]]$series.lin.coef.chng.x
# Weights pre tuned by random search. In alpha, beta, gamma order
pre.tuned.wts <- c(0.2148058, 0.2899638, 0.4952303)
pre.tuned.k <- 5
df <- data.frame(ex.series)
# Generate vector of time orders
df$t <- c(1:nrow(df))
# Generate vector of periods
nperiods <- simulation_master_list[[series.index]]$seasonal.periods
df$p <- rep(1:nperiods, length.out = nrow(df))
# Pull corresponding exogenous predictor(s)
X <- as.matrix(simulation_master_list[[series.index]]$x.chng)
XdistMetric <- "euclidean"
# Number of points to set aside for validation
val.len <- ifelse(nperiods == 12, nperiods, nperiods * 2)
# Calculate the weighted similarity matrix using Sw
Sw.ex <- SwMatrixCalc( # For the recency similarity St
t.in = df$t
# For the periodic similarity Sp
, p.in = df$p, nPeriods.in = nperiods
# For the exogenous similarity Sx
, X.in = X, XdistMetric.in = XdistMetric
# Weights to be applied to each similarity
, weights = pre.tuned.wts
)
# View the top corner of the weighted similarity matrix Sw
cat("\n Dimensions and Slice of S_w \n")
#>
#> Dimensions and Slice of S_w
print(dim(Sw.ex))
#> [1] 100 100
print(Sw.ex[1:5, 1:5])
#> 1 2 3 4 5
#> 1 0.9999999 0.5825337 0.4249690 0.4115130 0.5589633
#> 2 0.5825337 0.9999999 0.5989170 0.5690332 0.4841708
#> 3 0.4249690 0.5989170 0.9999999 0.6673498 0.4414853
#> 4 0.4115130 0.5690332 0.6673498 0.9999999 0.5582553
#> 5 0.5589633 0.4841708 0.4414853 0.5582553 0.9999999# Index we want to forecast
val.index <- c((length(ex.series) - val.len + 1):length(ex.series))
# Generate the forecast
knn.frcst <- knn.forecast(
Sim.Mat.in = Sw.ex,
f.index.in = val.index,
k.in = pre.tuned.k,
y.in = ex.series
)
In most cases you will likely want to tune the hyperparameters used
in the construction of S_w, and the number of nearest
neighbors, k, to consider for any given point. There are
many approaches that can be taken to accomplish this tuning, and many
users may choose to implement their preferred approach. However, for
those who want something pre-built I have included a simple tuning
function with the package called
knn.forecast.randomsearch.tuning. This function creates a
randomly generated Grid of potential sets of
hyperparameters
k,alpha,beta,gamma
and generates a forecast of length test.h on the last
test.h points in the series. The best set of parameters are
selected based on which row of the Grid led to the forecast
with the lowest MAPE (Mean Absolute Percent Error) over the points in
the forecast, and returned as the weight.opt and
k.opt items of the list object returned by the function.
Additionally, the ‘optimal’ similarity matrix to pass to
knn.forecast is also returned as Sw.opt, as
are the testing grid (Grid), best test MAPE
(Test.MAPE.opt), and the full vector of test MAPE values
(MAPE.all) corresponding to each row in
Grid.
If you do not want to tune the hyperparameters on the entire series
and prefer to leave some points for validation of the tuned result the
val.holdout.len will remove that many points from the end
of the series, and will perform the test forecasts on the
test.h points at the end of the series after the validation
observations are removed.
Using the example series from the previous section, we can reproduce the ‘pre-tuned’ weights from the previous section and generate a forecast using the included tuning function.
# Calculate component similarity matrices
St.ex <- StMatrixCalc(df$t)
Sp.ex <- SpMatrixCalc(df$p, nPeriods = nperiods)
Sx.ex <- SxMatrixCalc(X)
# Set seed for reproducibility
set.seed(10)
# Run tuning function
tuning.ex <- knn.forecast.randomsearch.tuning(
grid.len = 10**4,
y.in = ex.series,
St.in = St.ex,
Sp.in = Sp.ex,
Sx.in = Sx.ex,
test.h = val.len,
max.k = NA,
val.holdout.len = val.len
)
cat("\n Tuned Hyperparameters \n")
#>
#> Tuned Hyperparameters
cat("\n S_w Weights \n")
#>
#> S_w Weights
print(tuning.ex$weight.opt)
#> [1] 0.2148058 0.2899638 0.4952303
cat("\n k \n")
#>
#> k
print(tuning.ex$k.opt)
#> [1] 5
# Pull out tuned S_w and k
k.opt.ex <- tuning.ex$k.opt
Sw.opt.ex <- tuning.ex$Sw.opt# Generate the forecast
knn.frcst.tuned <- knn.forecast(
Sim.Mat.in = Sw.opt.ex,
f.index.in = val.index,
k.in = k.opt.ex,
y.in = ex.series
)
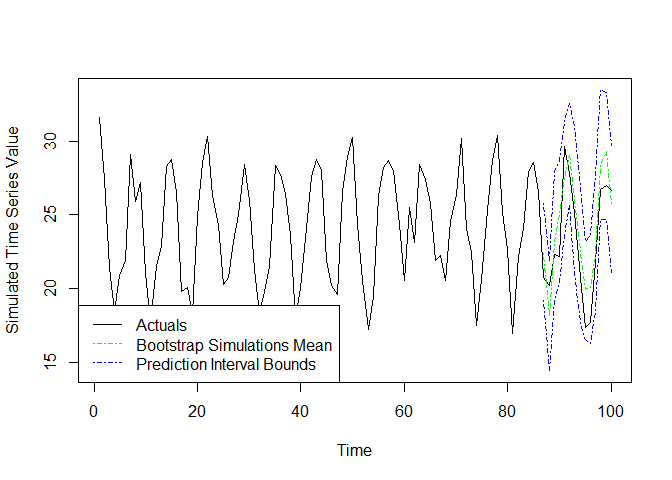
The methodology used to produce forecasts with prediction intervals
in this package is based on the description of “Prediction intervals
from bootstrapped residuals” from chapter 5.5 of Hyndman R,
Athanasopoulos G (2021) https://otexts.com/fpp3/prediction-intervals.html#prediction-intervals-from-bootstrapped-residuals,
modified as needed for use with KNN regression. The function
knn.forecast.boot.intervals is used to implement this
method. The algorithm employed starts by calculating a pool of forecast
errors to later sample from. If there are n points prior to
the first observation indicated in f.index.in then there
will be n - k.in errors generated by one-step ahead
forecasts starting with the point of the response series at the index
k.in + 1. The first k.in points cannot be
estimated because a minimum of k.in eligible neighbors
would be needed. The optional burn.in argument can be used
to increase the number of points from the start of the series that need
to be available as neighbors before calculating errors for the pool.
Next, B possible paths the series could take are simulated
using the pool of errors. Each path is simulated by calling
knn.forecast, estimating the first point in
f.index.in, adding a sampled forecast error, then adding
this value to the end of the series. This process is then repeated for
the next point in f.index.in until all have been estimated.
The final output interval estimates are calculated for each point in
f.index.in by taking the appropriate percentiles of the
corresponding simulations of that point. The output is returned as a
list with the upper and lower prediction interval bounds based on the
supplied confidence level, as well as the mean and median of the
simulated points for each observation in the forecast index. All
B simulations can be returned if desired using the optional
return.simulations = TRUE argument. Below we have an
example, where we generate an interval forecast at the 95% confidence
level, and plot the results. Note that the mean forecast from this
function may differ from the point forecast generated by
knn.forecast. This difference is driven by the random
sampling of residuals to generate the simulated paths, as well as the
behavior of adding simulated points in a given path to the list of
eligible neighbors when repeatably calling
knn.forecast.
# Produce interval forecast list
interval.forecast <- knn.forecast.boot.intervals(
Sim.Mat.in = Sw.opt.ex,
f.index.in = val.index,
y.in = ex.series,
k.in = k.opt.ex
)
# Pull out desired components
lb <- interval.forecast$lb
ub <- interval.forecast$ub
mean.boot <- interval.forecast$mean